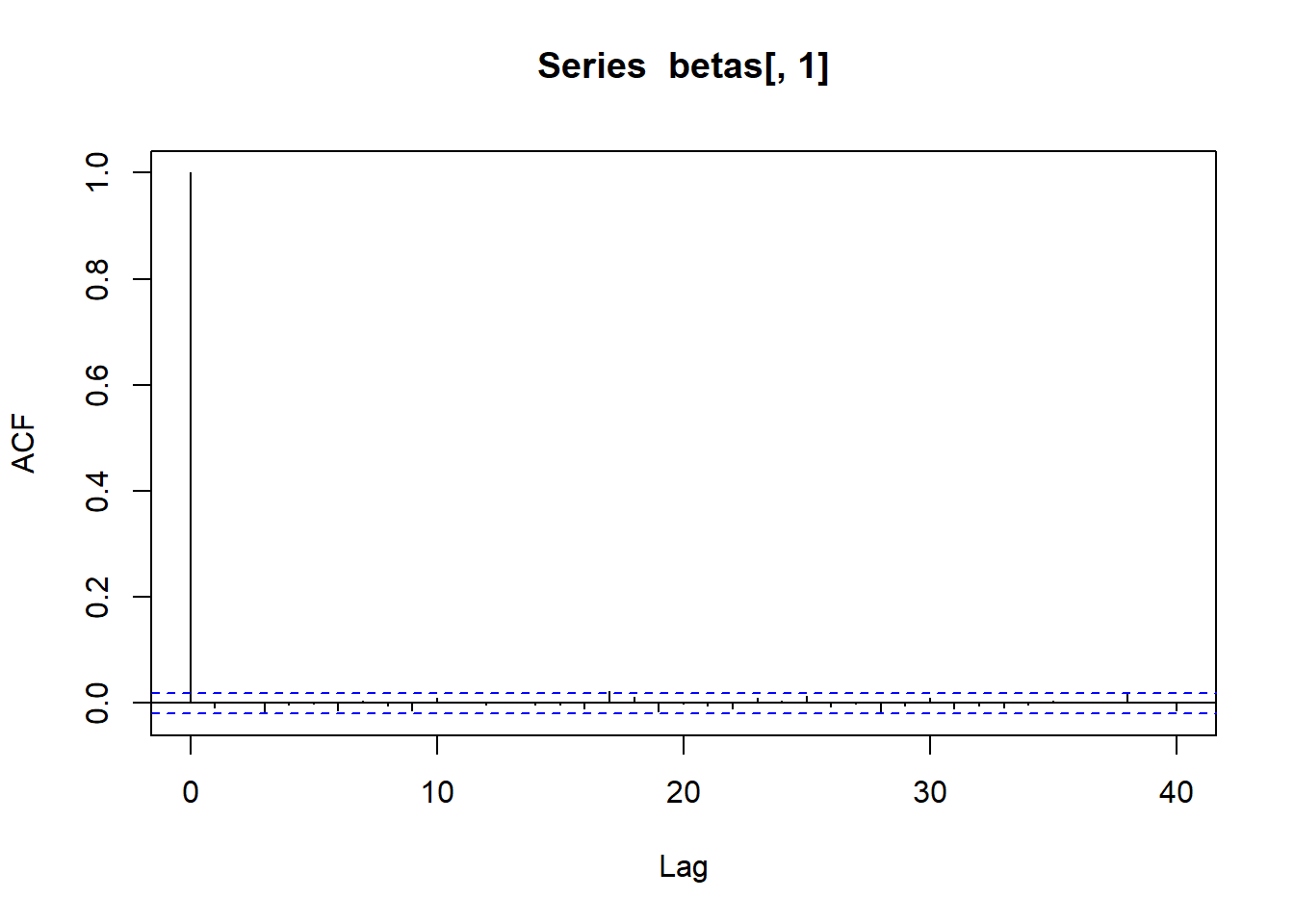Script 5 - MCMC - Stan

Author

Roberto Ascari

You can download the R script here.

Some useful links for working with Stan:

List of Language-Specific Stan Interfaces.
Rstan: an interface to Stan for R.
RStan: Getting Started.

Linear Regression

In this part, we are going to fit a simple linear regression model through Stan. Here you can download the .stan model.

First of all, let’s compile the model and save it into an R object.

LM_Model <- rstan::stan_model(file="data/LM_Model.stan")

LM_Model

S4 class stanmodel 'anon_model' coded as follows:
data{
    int<lower = 0> n;  // number of obs
    int<lower = 0> K;  // number of covariates (including the intercept)

    vector[n] y;     // response
    matrix[n, K] X;  // covariates
  real a0;
  real b0;
    vector[K] beta0;
    vector[K] s2_0;
}
parameters{
    real<lower = 0> sigma2;
    vector[K] beta;
}
transformed parameters {
    vector[n] mu;
  mu = X * beta;
}
model{
    // Prior:
    sigma2 ~ inv_gamma(a0, b0);

    for(k in 1:K){
        beta[k] ~ normal(beta0[k], sqrt(s2_0[k]));
    }
    // Likelihood:
    y ~ normal(mu, sqrt(sigma2));
}
generated quantities{

    vector[n] log_lik;

    for (j in 1:n){
            log_lik[j] = normal_lpdf(y[j] | mu[j], sqrt(sigma2));
    }
}

We consider the Prestige data from the car package. Statistical units are occupations, for which we have:

education: average education of occupational incumbents, years, in 1971;
income: average income of incumbents, dollars, in 1971;
women: percentage of incumbents who are women;
prestige: Pineo-Porter prestige score for occupation, from a social survey conducted in the mid-1960s;
census: canadian Census occupational code;
type: type of occupation (bc, Blue Collar; prof, Professional, Managerial, and Technical; wc, White Collar).

Let’s transform the income variable so to reduce the asimmetry.

data("Prestige")

Prestige2 <-
  Prestige[complete.cases(Prestige),-5]
Prestige2$income <- log(Prestige2$income)

In order to fit the stan model, we need to pass some data: - y: the response vector;

X: the design matrix;
n: the sample size;
K: the number of covariates (including the intercept term);
a0, b0, beta0, s2_0: hyperparameters.

y <- Prestige2$prestige
mod <- lm(prestige ~ ., data=Prestige2)

X <- model.matrix(mod)
n <- nrow(X)
K <- ncol(X)

We further create a list containing the objects to be passed to the stan model.

data.stan <- list(
  y = y,
  X = X,
  n = n,
  K = K,
  a0 = 10,
  b0 = 10,
  beta0 = rep(0, K),
  s2_0 = rep(10, K)
)

We can now use the rstan::sampling function to fit the model. We what two chains, each of length 10’000, and we want to discard the first 50% as warm-up.

n.iter <- 10000
nchain <- 2

LM_stan <- rstan::sampling(
  object = LM_Model,
  data = data.stan,
  warmup = 0.5*n.iter, 
  iter = n.iter,
  thin=1, chains = nchain,
  refresh = n.iter/2     
  #, pars=c("beta", "sigma2")
  )


SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 7.1e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.71 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: Iteration:    1 / 10000 [  0%]  (Warmup)
Chain 1: Iteration: 5000 / 10000 [ 50%]  (Warmup)
Chain 1: Iteration: 5001 / 10000 [ 50%]  (Sampling)
Chain 1: Iteration: 10000 / 10000 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 1.551 seconds (Warm-up)
Chain 1:                1.887 seconds (Sampling)
Chain 1:                3.438 seconds (Total)
Chain 1: 

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 2).
Chain 2: 
Chain 2: Gradient evaluation took 1.3e-05 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.13 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2: 
Chain 2: 
Chain 2: Iteration:    1 / 10000 [  0%]  (Warmup)
Chain 2: Iteration: 5000 / 10000 [ 50%]  (Warmup)
Chain 2: Iteration: 5001 / 10000 [ 50%]  (Sampling)
Chain 2: Iteration: 10000 / 10000 [100%]  (Sampling)
Chain 2: 
Chain 2:  Elapsed Time: 1.666 seconds (Warm-up)
Chain 2:                1.78 seconds (Sampling)
Chain 2:                3.446 seconds (Total)
Chain 2:

summ <- summary(LM_stan, pars = c("beta", "sigma2"))$summary

rownames(summ)[1:K] <- colnames(X)
round(summ, 3)

              mean se_mean    sd   2.5%    25%    50%    75%  97.5%    n_eff
(Intercept) -2.968   0.041 3.166 -9.251 -5.121 -2.989 -0.828  3.335 6073.251
education    4.306   0.007 0.452  3.431  3.997  4.309  4.608  5.183 4014.248
income       0.507   0.010 0.618 -0.689  0.081  0.505  0.925  1.712 4123.754
women       -0.060   0.000 0.025 -0.108 -0.076 -0.060 -0.044 -0.012 6170.313
typeprof     6.119   0.034 2.255  1.602  4.600  6.131  7.615 10.485 4498.555
typewc      -2.776   0.024 1.791 -6.340 -3.971 -2.789 -1.575  0.760 5570.694
sigma2      48.765   0.079 6.868 37.081 43.948 48.202 52.919 63.777 7574.694
            Rhat
(Intercept)    1
education      1
income         1
women          1
typeprof       1
typewc         1
sigma2         1

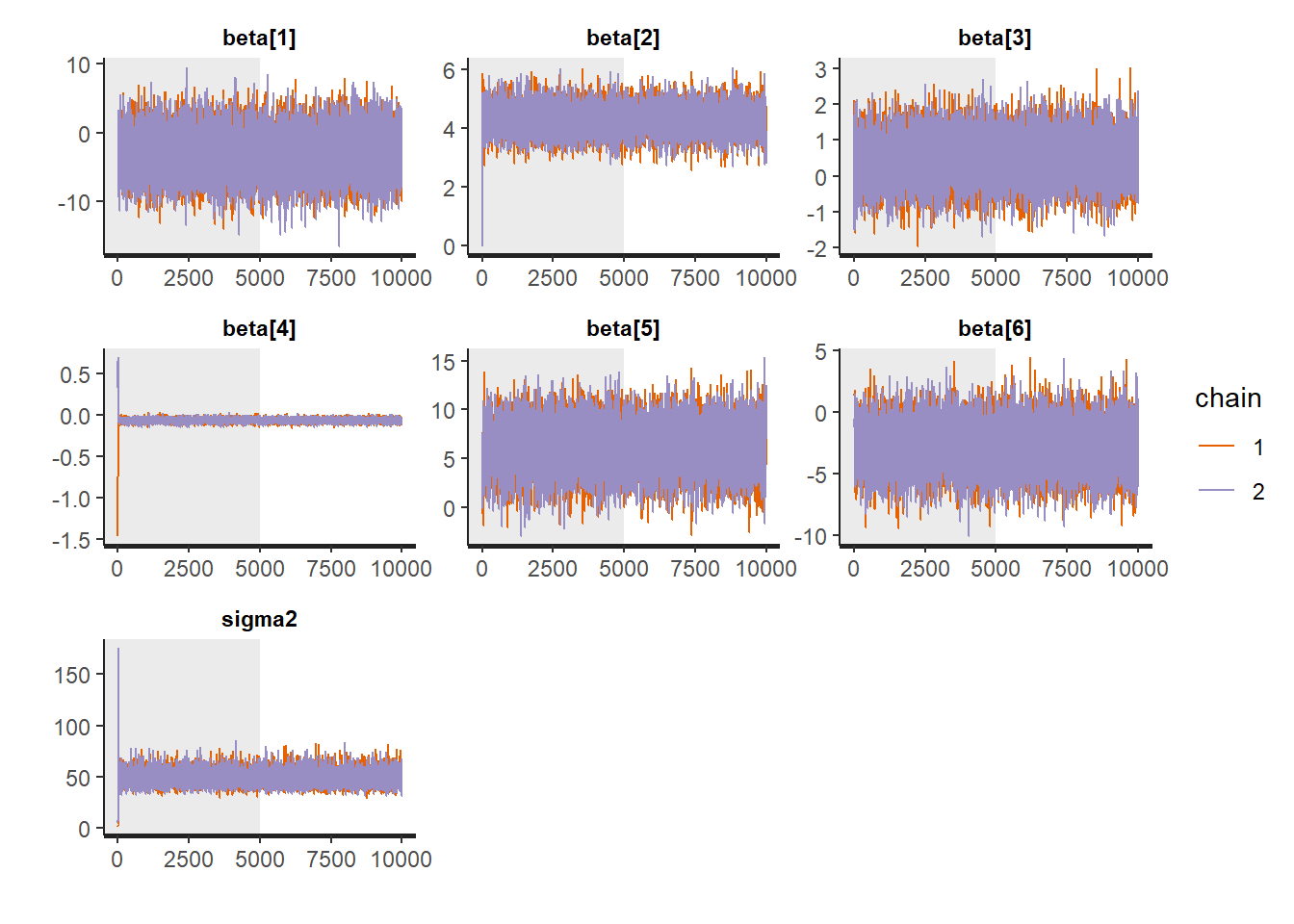
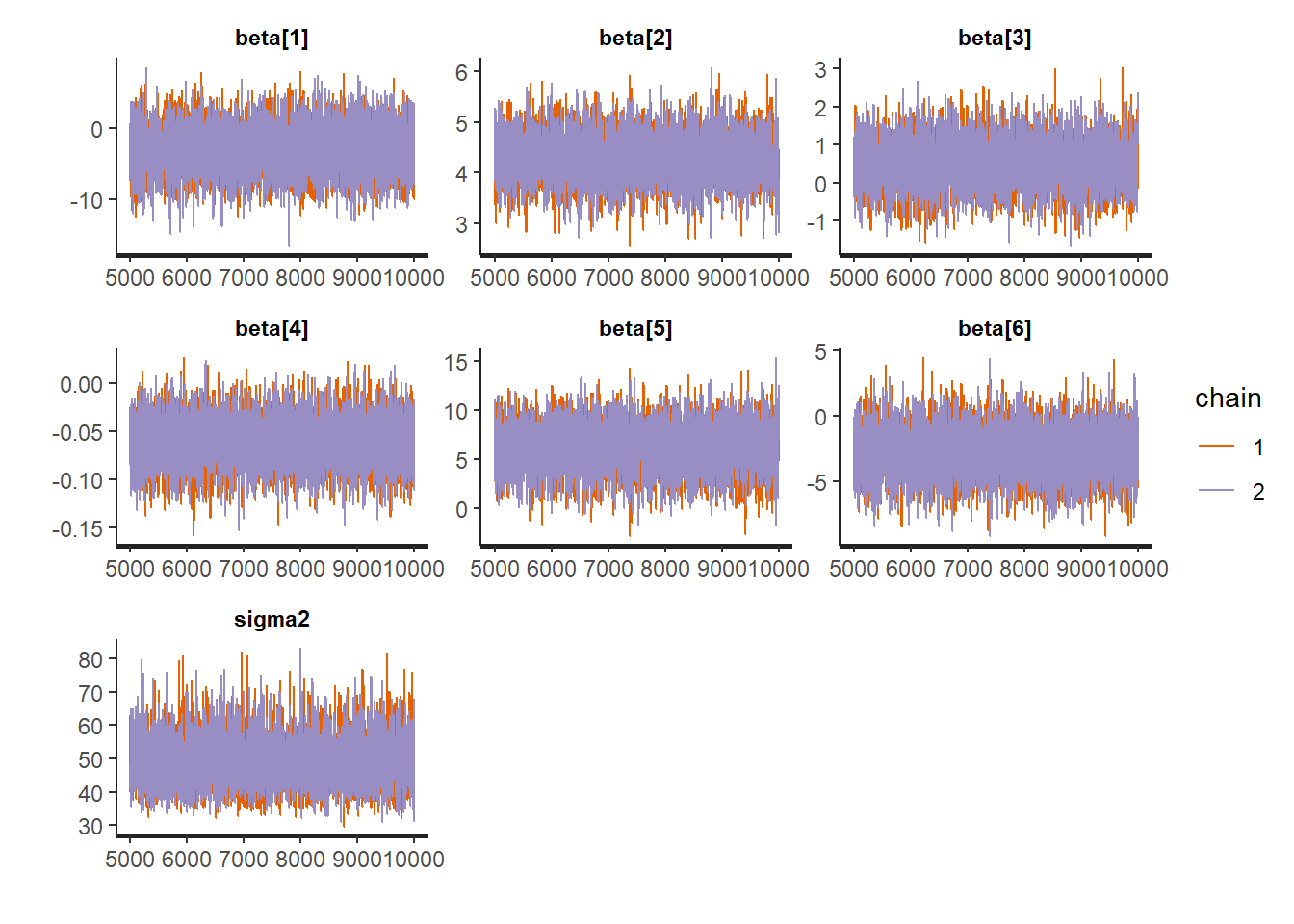
Traceplots:

rstan::traceplot(LM_stan, pars = c('beta', 'sigma2'), inc_warmup = TRUE)

rstan::traceplot(LM_stan, pars = c('beta', 'sigma2'), inc_warmup = FALSE)

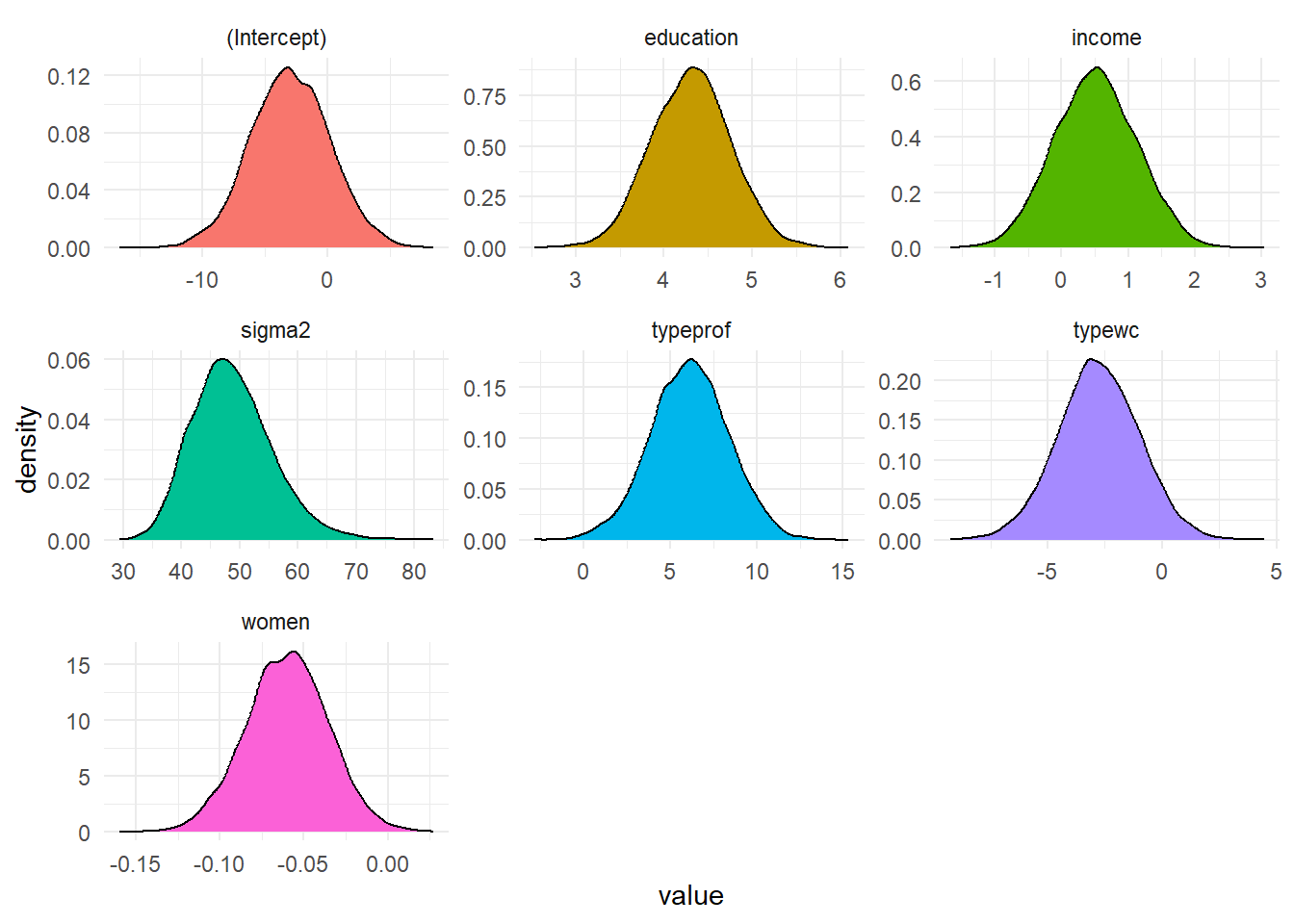
post_chain <- rstan::extract(LM_stan, c('beta', 'sigma2')) 
betas <- post_chain$beta
colnames(betas) <- colnames(X)

sigma2 <- post_chain$sigma2

df_plot <- 
  data.frame(value = c(
    betas[,1], betas[,2], betas[,3],
    betas[,4], betas[,5], betas[,6],
    sigma2), 
    param = rep(c(colnames(X), 'sigma2'), 
                each = nrow(post_chain$beta)))


df_plot %>% 
  ggplot(aes(value, fill = param)) + 
  geom_density() + 
  facet_wrap(~param, scales = 'free') + 
  theme_minimal() + 
  theme(legend.position="false")

acf(betas[,1])

acf(betas[,2])

acf(betas[,3])

acf(betas[,4])

acf(betas[,5])

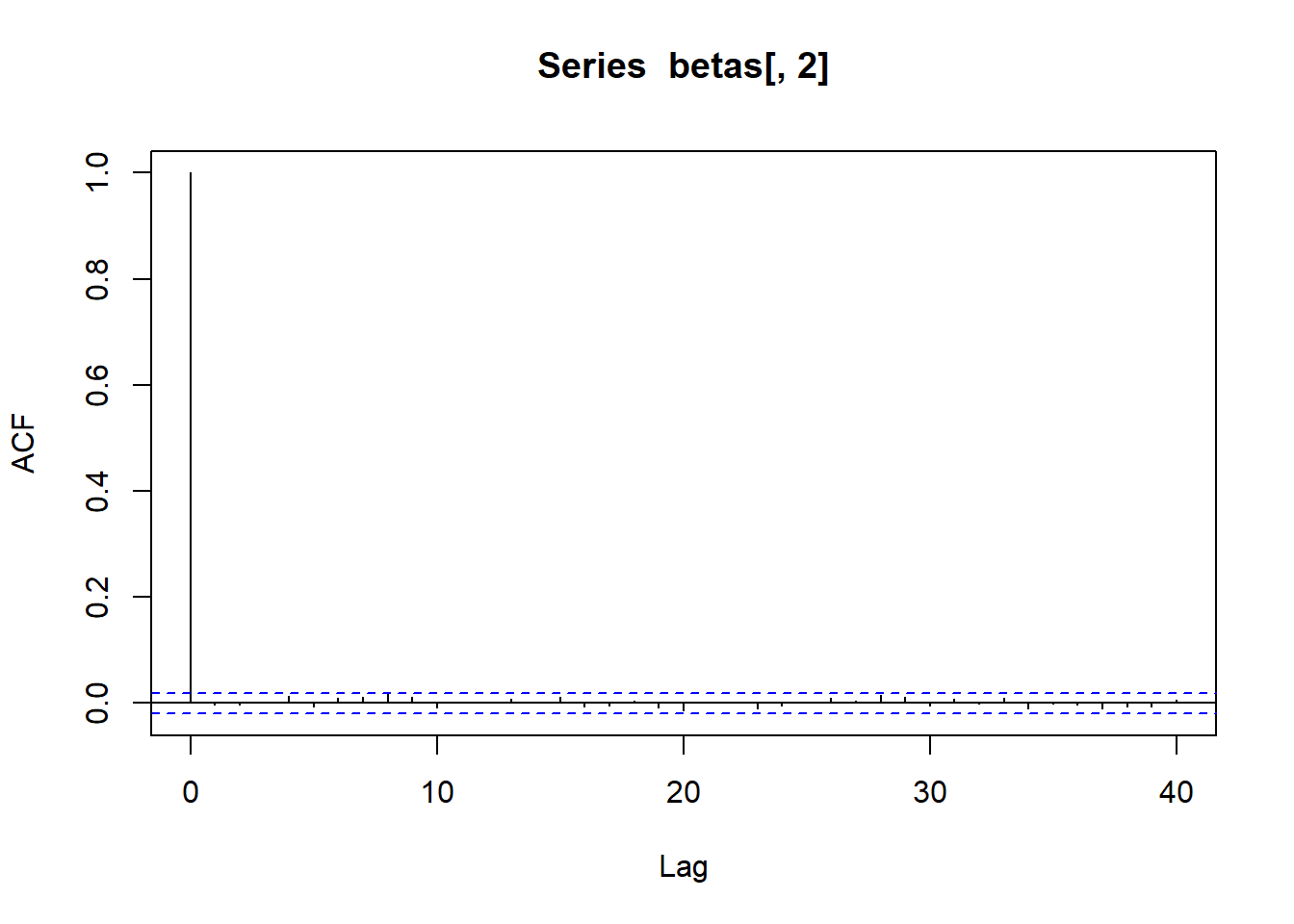
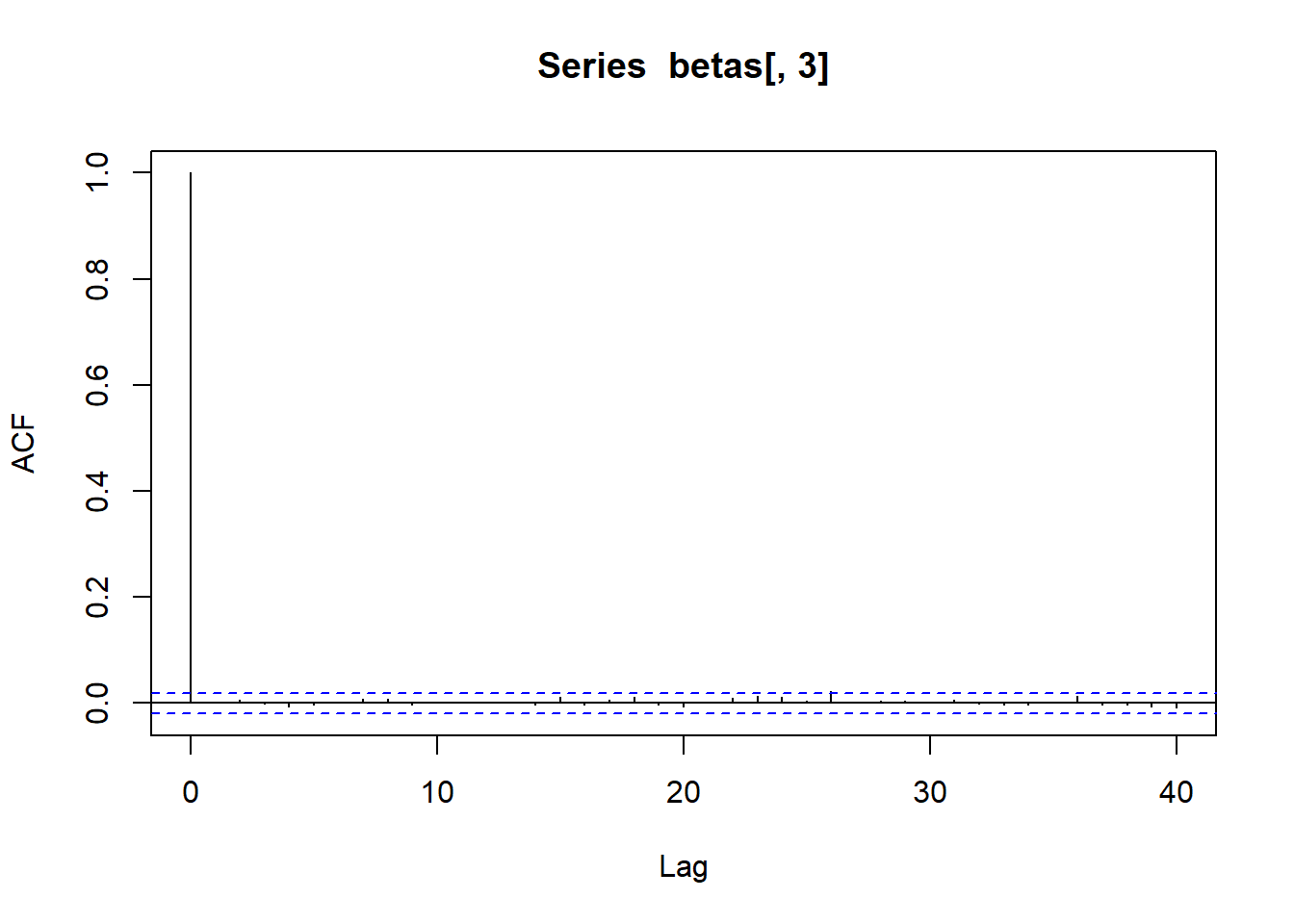
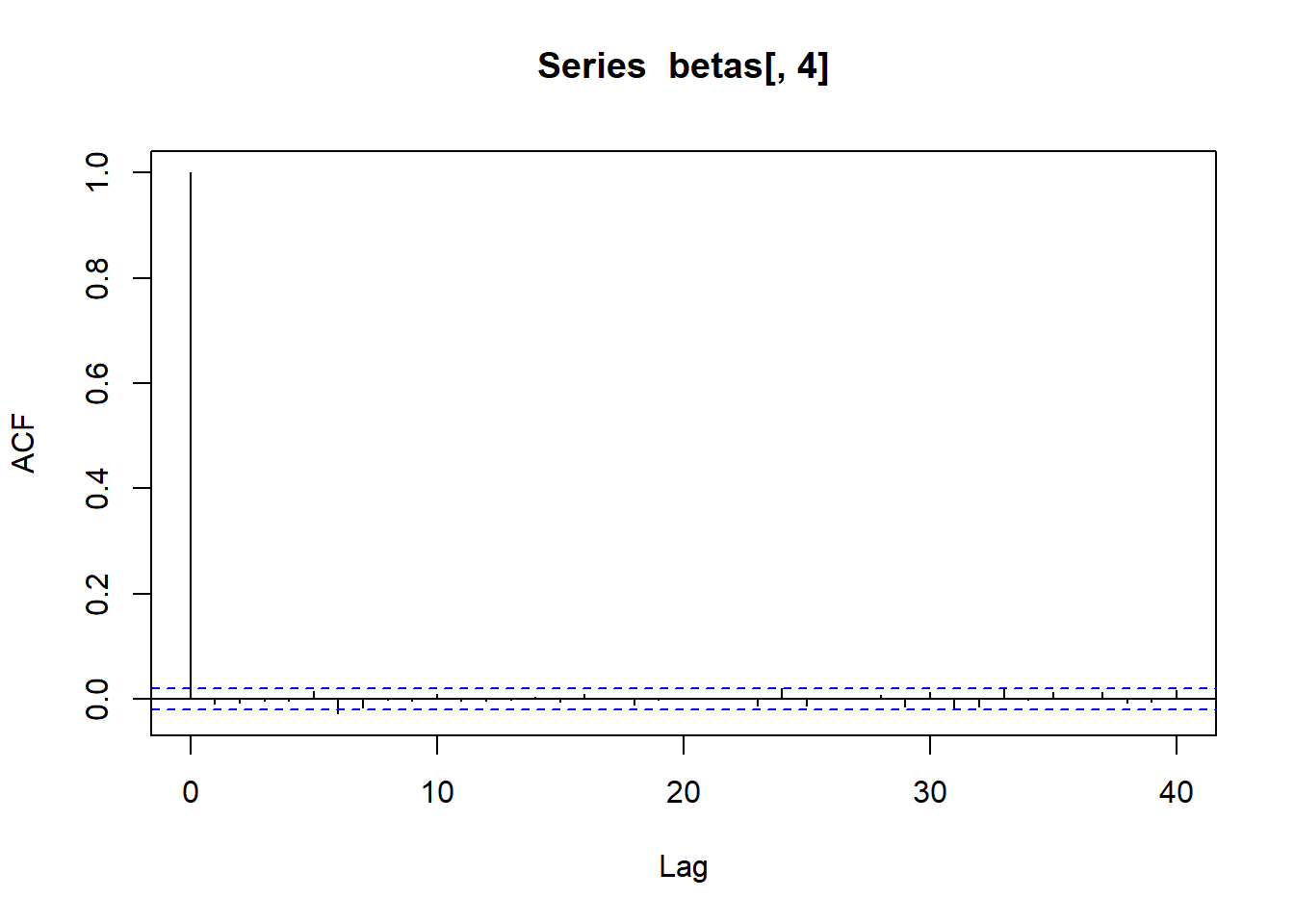
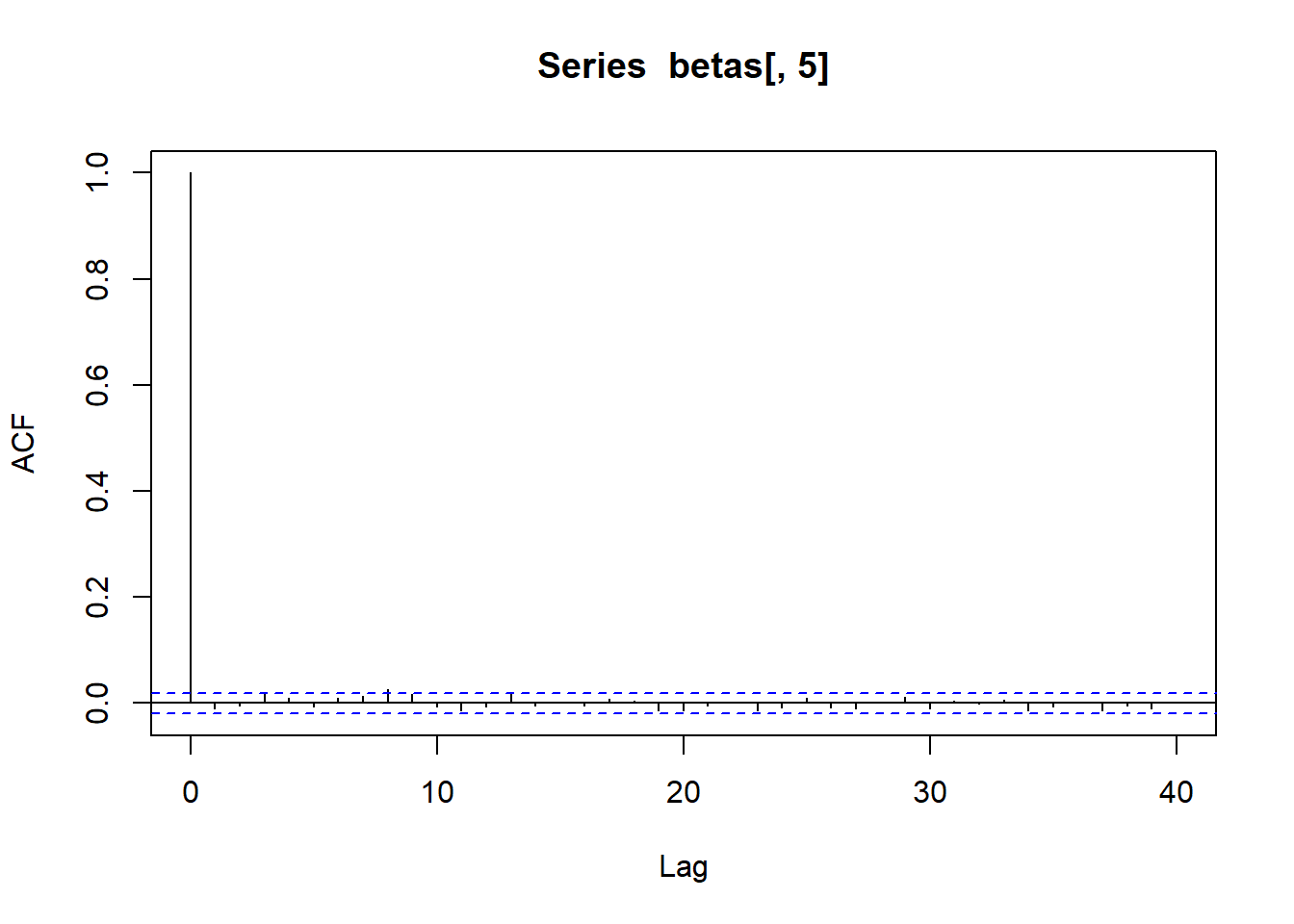
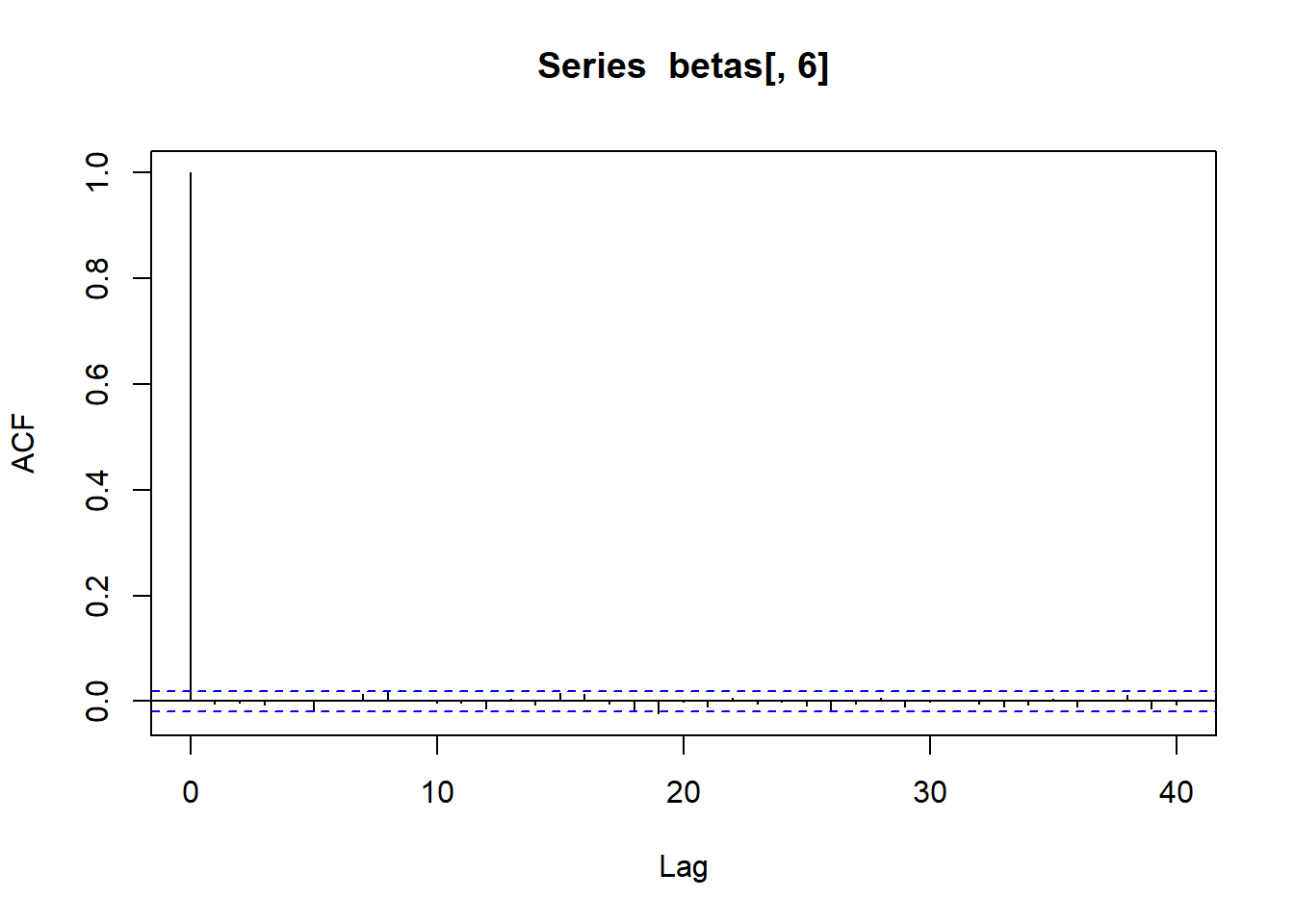
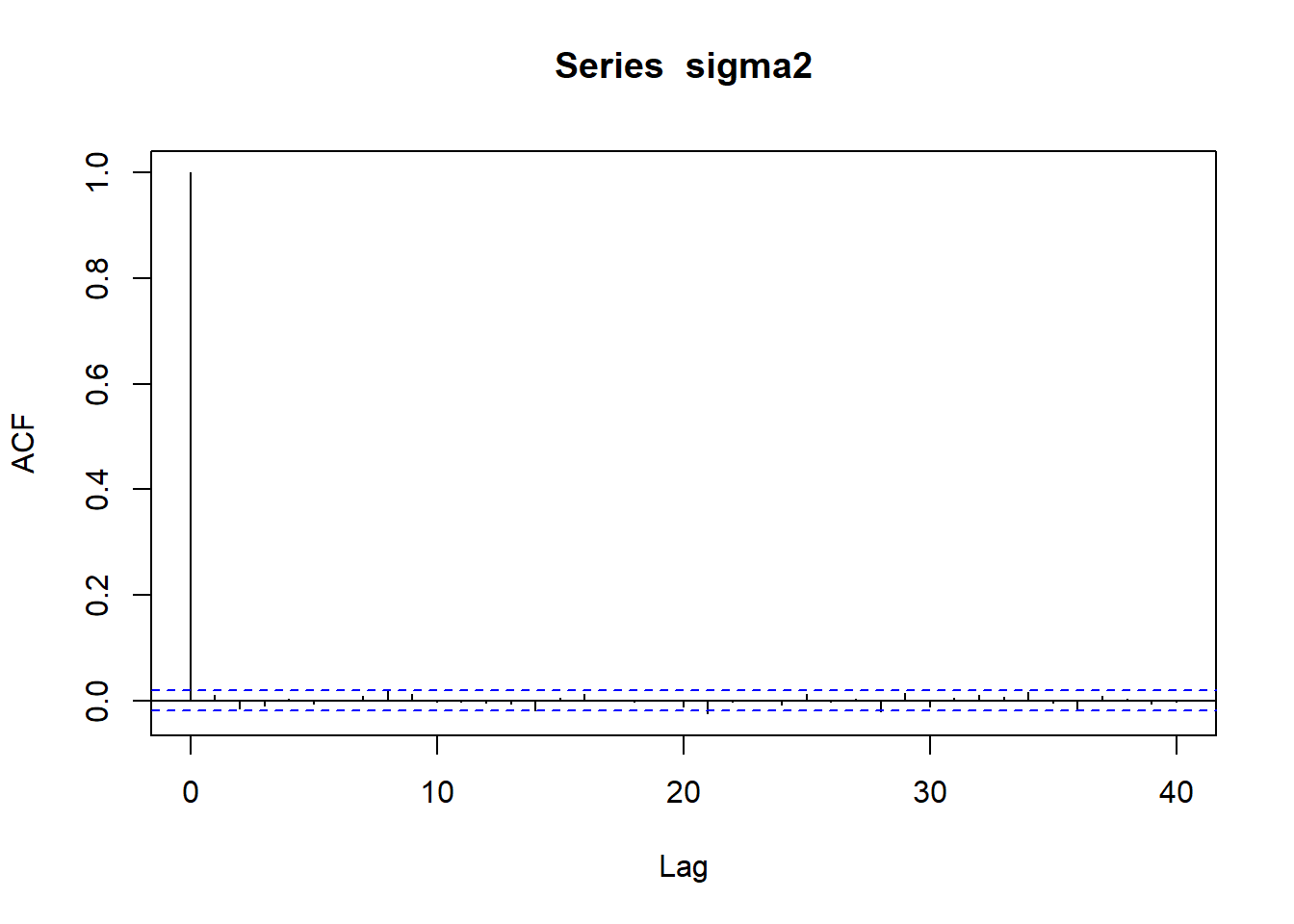
acf(betas[,5])
acf(betas[,6])

acf(sigma2)

As classical MCMCs, we can use the sampled values to approximate any quantity of interest. For example, we can approximate \(\mathbb{P}(\beta_1 > 4, \beta_3 > -0.5)\):

mean(betas[,2] > 4 & betas[,4] > -.5)

[1] 0.7481

Logistic Regression

Let’s consider the logistic regression model to the cardiac dataset.

The Logistic_Model.stan model can be downloaded here.

rm(list = ls())
cardiac <- read.csv("data/cardiac.csv", header=T, sep=";")

y <- cardiac$Chd
X <- model.matrix(lm(Chd ~ ., data=cardiac))
n <- nrow(X)
K <- ncol(X)

Logistic_Model <-
  rstan::stan_model(file="data/Logistic_Model.stan")

Logistic_Model

S4 class stanmodel 'anon_model' coded as follows:
///////////////////////// DATA /////////////////////////////////////
data {
    int<lower = 1> n;       // number of data
    int<lower = 1> K;       // number of covariates (including the intercept)
    int<lower = 0, upper = 1> y[n];   // response vector
    matrix[n, K] X;           // design matrix

  vector[K] beta0;
  vector[K] s2_0;
}
//////////////////// PARAMETERS /////////////////////////////////
parameters {
    vector[K] beta;        // regression coefficients
}
transformed parameters {
    vector[n] eta;
    vector<lower=0>[n] Odds;
    vector<lower=0,upper=1>[n] p;

  eta = X * beta;

  for(i in 1:n){
    Odds[i] = exp(eta[i]);
    p[i] = Odds[i]/(1+Odds[i]);
  }

}
////////////////// MODEL ////////////////////////
model {
  // Prior
    for (j in 1:K){
        beta[j] ~ normal(beta0, sqrt(s2_0));
    }

  // Likelihood
    for (s in 1:n){
        y[s] ~ bernoulli(p[s]);
    }
}

data.stan_logis <- list(
  y = y,
  X = X,
  n = n,
  K = K,
  beta0 = rep(0, K),
  s2_0 = rep(10, K)
)

n.iter <- 10000
nchain <- 2

Logistic_stan <- rstan::sampling(
  object = Logistic_Model,
  data = data.stan_logis,
  warmup = 0.5*n.iter, iter = n.iter,
  thin = 1, chains = nchain,
  refresh = n.iter/2
)


SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 0.000102 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 1.02 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: Iteration:    1 / 10000 [  0%]  (Warmup)
Chain 1: Iteration: 5000 / 10000 [ 50%]  (Warmup)
Chain 1: Iteration: 5001 / 10000 [ 50%]  (Sampling)
Chain 1: Iteration: 10000 / 10000 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 2.21 seconds (Warm-up)
Chain 1:                1.592 seconds (Sampling)
Chain 1:                3.802 seconds (Total)
Chain 1: 

SAMPLING FOR MODEL 'anon_model' NOW (CHAIN 2).
Chain 2: 
Chain 2: Gradient evaluation took 2.5e-05 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.25 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2: 
Chain 2: 
Chain 2: Iteration:    1 / 10000 [  0%]  (Warmup)
Chain 2: Iteration: 5000 / 10000 [ 50%]  (Warmup)
Chain 2: Iteration: 5001 / 10000 [ 50%]  (Sampling)
Chain 2: Iteration: 10000 / 10000 [100%]  (Sampling)
Chain 2: 
Chain 2:  Elapsed Time: 1.756 seconds (Warm-up)
Chain 2:                1.647 seconds (Sampling)
Chain 2:                3.403 seconds (Total)
Chain 2:

summ <- summary(Logistic_stan, pars = "beta")$summary
rownames(summ)[1:K] <- colnames(X)
round(summ, 3)

              mean se_mean    sd   2.5%    25%    50%    75%  97.5%    n_eff
(Intercept) -4.431   0.021 0.952 -6.331 -5.064 -4.402 -3.776 -2.654 1974.032
Age          0.093   0.000 0.020  0.053  0.079  0.092  0.106  0.133 1973.055
             Rhat
(Intercept) 1.002
Age         1.002

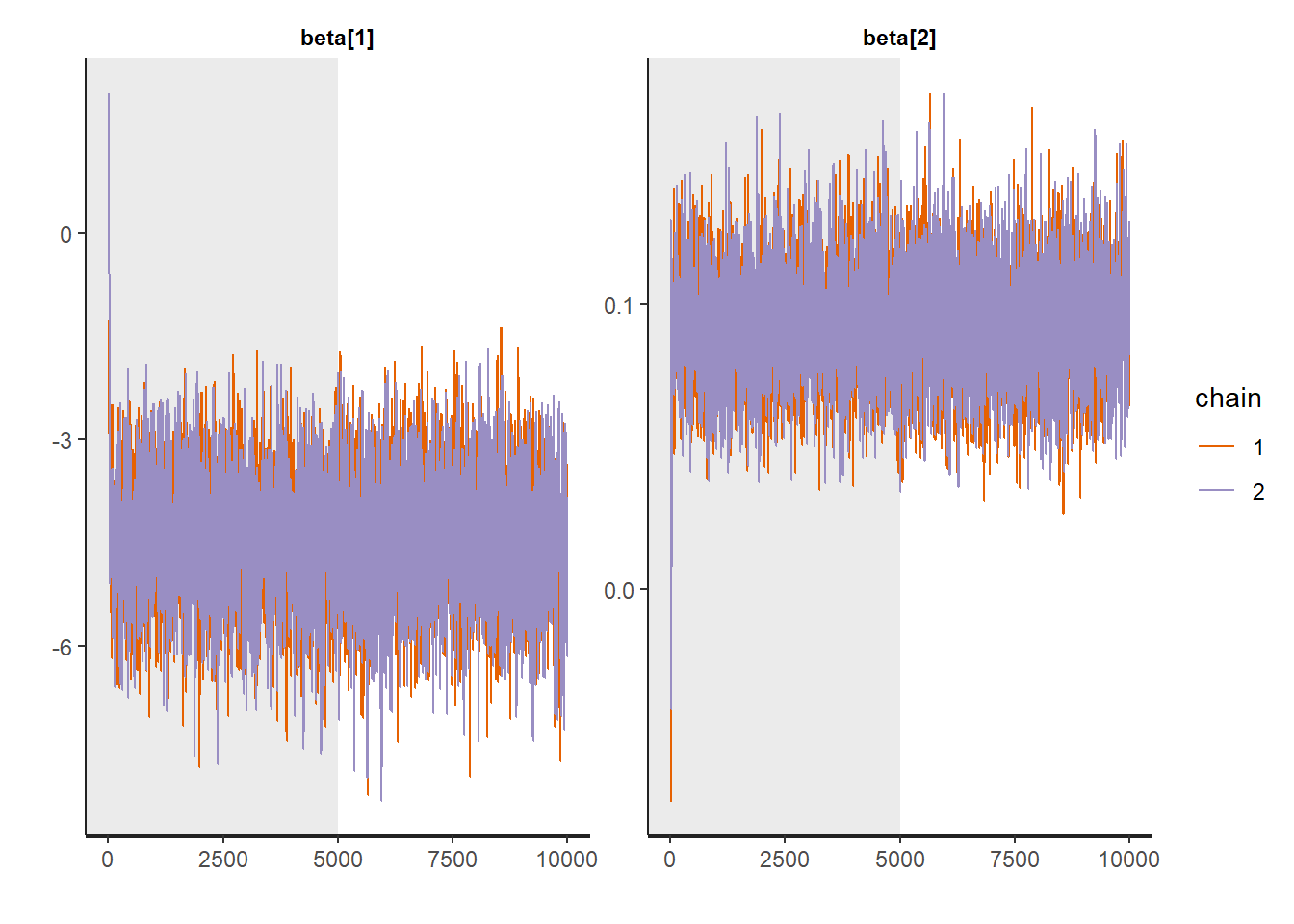
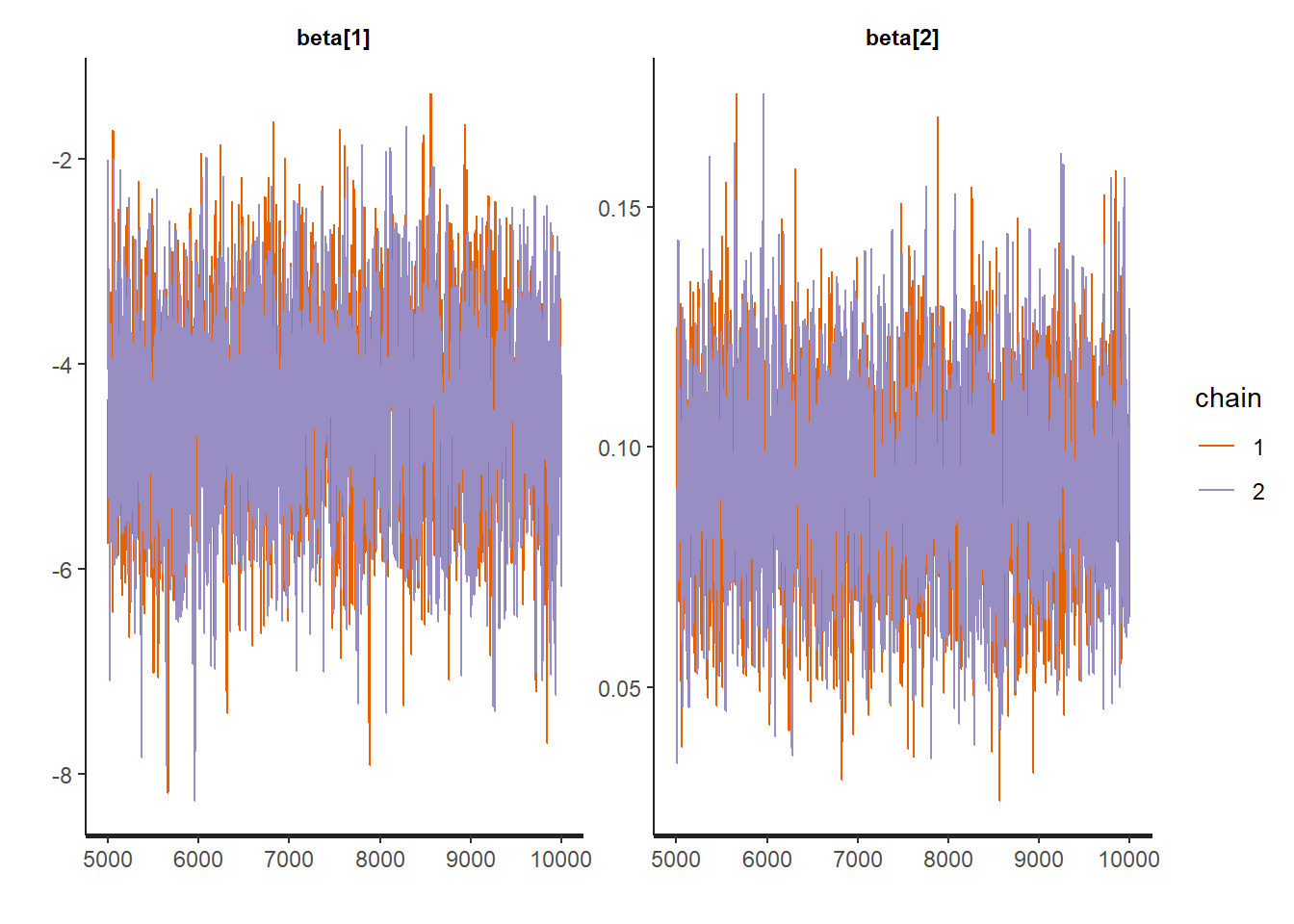
rstan::traceplot(Logistic_stan, pars = "beta", inc_warmup = TRUE)

rstan::traceplot(Logistic_stan, pars = "beta", inc_warmup = FALSE)

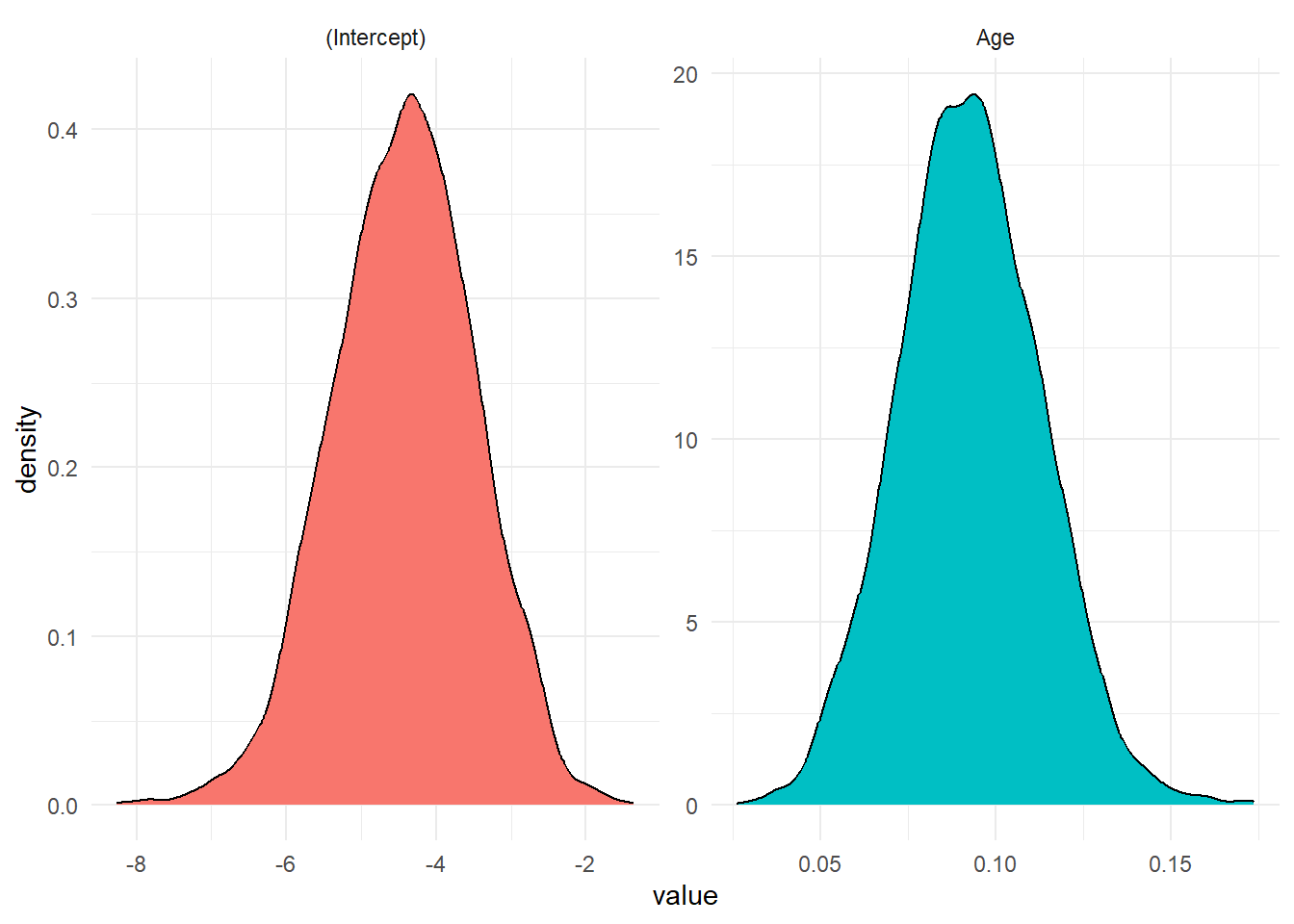
post_chain <- rstan::extract(Logistic_stan, "beta") 
betas <- post_chain$beta
colnames(betas) <- colnames(X)

df_plot <- 
  data.frame(value = c(betas[,1], betas[,2]), 
             param = rep(colnames(X), each = nrow(post_chain$beta)))

df_plot %>% 
  ggplot(aes(value, fill = param)) + 
  geom_density() + 
  facet_wrap(~param, scales = 'free') + 
  theme_minimal() + 
  theme(legend.position="false")

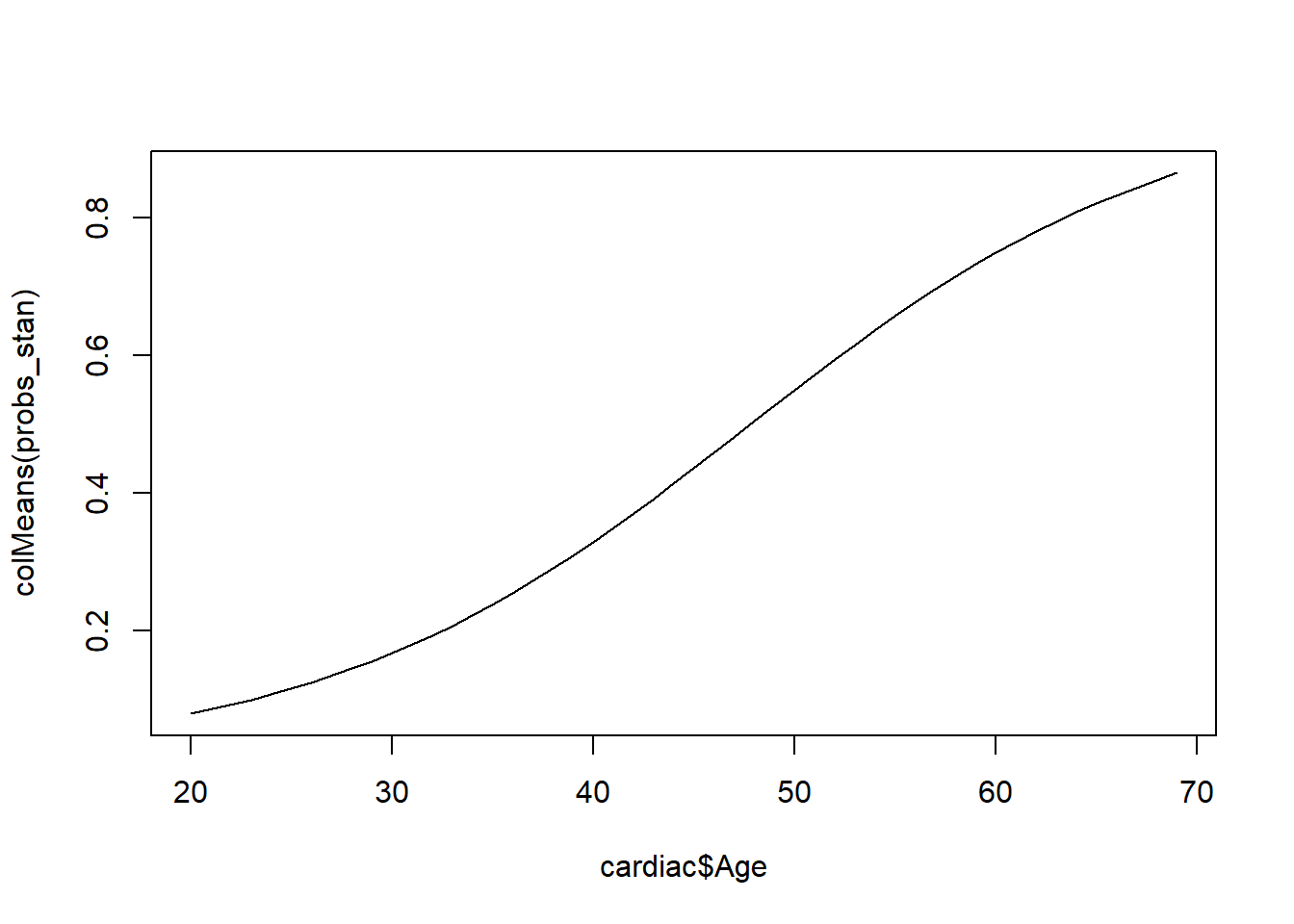
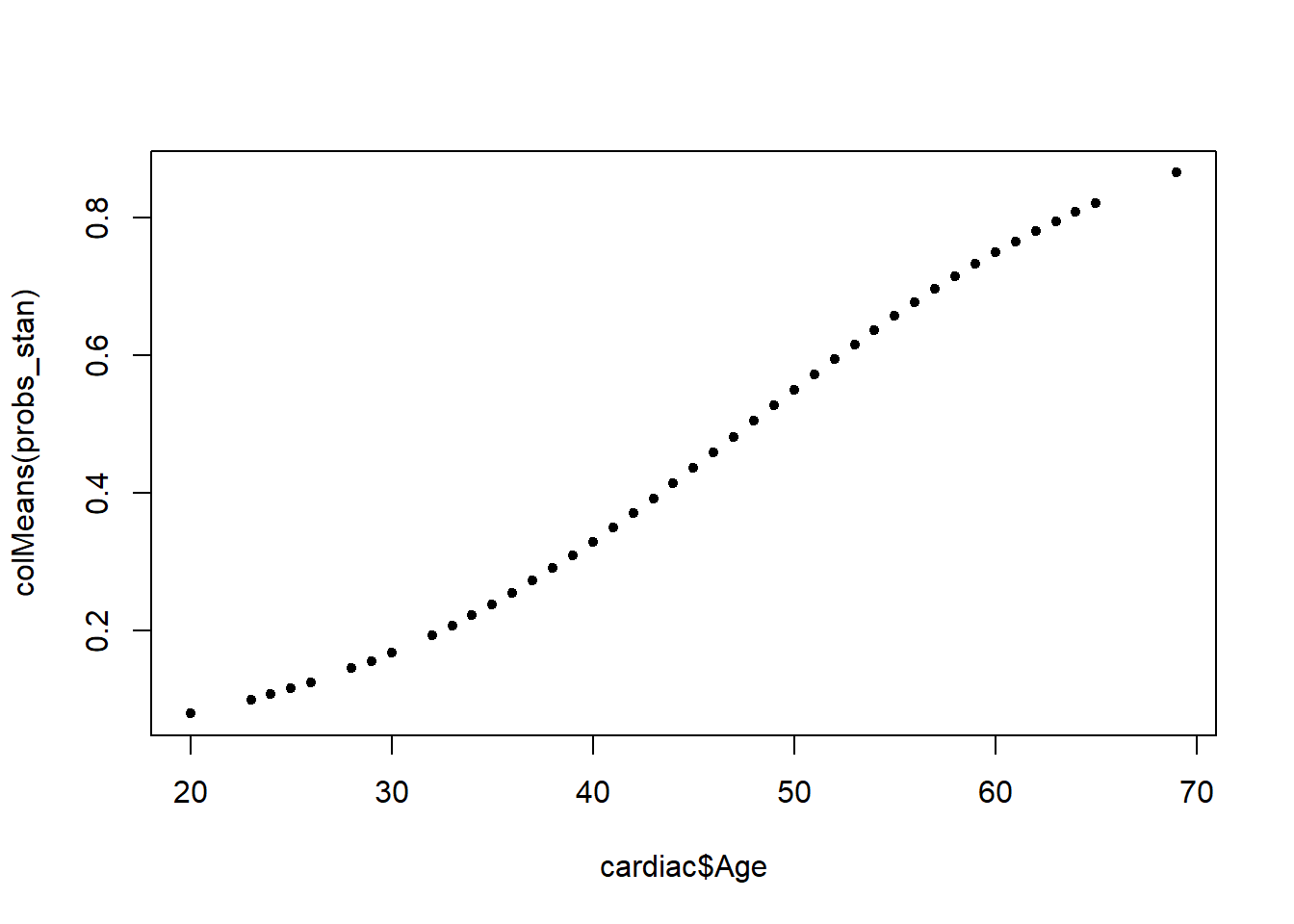
We can evaluate probabilities for each patients.

probs_stan <- rstan::extract(Logistic_stan, "p")$p
plot(cardiac$Age, colMeans(probs_stan), pch=20, type="l")

plot(cardiac$Age, colMeans(probs_stan), pch=20)